Retrospective Simulation in Buying and selling: Testing Methods Past Realized Worth Paths

By Mahavir Bhattacharya

TL;DR:

This weblog introduces retrospective simulation, impressed by Taleb’s “Fooled by Randomness,” to simulate 1,000 alternate historic worth paths utilizing a non-parametric Brownian bridge technique. Utilizing SENSEX knowledge (2000–2020) as in-sample knowledge, the creator optimises an EMA crossover technique throughout the in-sample knowledge first, after which applies it to the out-of-sample knowledge utilizing the optimum parameters obtained from the in-sample backtest. Whereas the technique outperforms the buy-and-hold method in in-sample testing, it considerably underperforms in out-of-sample testing (2020–2025), highlighting the danger of overfitting to a single realised path. The creator then runs the backtest throughout all simulated paths to establish probably the most ceaselessly profitable SEMA-LEMA parameter combos.

The creator additionally calculates VaR and CVaR utilizing over 5 million simulated returns and compares return extremes and distributional traits, revealing heavy tails and excessive kurtosis. This framework allows extra strong technique validation by evaluating how methods may carry out throughout a number of believable market situations.

Introduction

In “Fooled by Randomness”,  Taleb says at one place, “To start with, once I knew near nothing (that’s, even lower than at present), I puzzled whether or not the time collection reflecting the exercise of individuals now lifeless or retired ought to matter for predicting the longer term.”

This bought me pondering. We regularly run simulations for the possible paths a time collection can take sooner or later. Nevertheless, the premise for these simulations is predicated on historic knowledge. Given the stochastic nature of asset costs (learn extra), the realised worth path had the selection of an infinite variety of paths it may have taken, but it surely traversed via solely a kind of infinite prospects. And I believed to myself, why not simulate these alternate paths?

In widespread apply, this method is known as bootstrap historic simulation. I selected to check with it as retrospective simulation, as a extra intuitive counterpart to the phrases ‘look-ahead’ and ‘walk-forward’ used within the context of simulating the longer term.

Article map

Right here’s an overview of how this text is laid out:

Information Obtain

We import the required libraries and obtain the day by day knowledge of the SENSEX index, a broad market index primarily based on the Bombay Inventory Trade of India.

I’ve downloaded the information from January 2000 to November 2020 because the in-sample knowledge, and from December 2020 to April 2025 because the out-of-sample knowledge. We may have put in a niche (an embargo) between the in-sample and out-of-sample knowledge to minimise, if not get rid of, knowledge leakage (learn extra). In our case, there’s no direct knowledge leakage. Nevertheless, since inventory ranges (costs) are recognized to bear autocorrelation, like we noticed above, the SENSEX index on the primary buying and selling day of December 2020 could be extremely correlated with its stage on the final buying and selling day of November 2020.

Thus, once we prepare our mannequin on knowledge that features the final buying and selling day of November 2020, it extracts data from that day’s stage and makes use of it to get skilled. Since our testing dataset is from the primary buying and selling day of December 2020, some residual data from the coaching dataset is current within the testing dataset.

As an extension, the coaching set accommodates some data that can also be current within the testing dataset. Nevertheless, this data will diminish over time and finally turn out to be insignificant. Having mentioned that, I didn’t keep a niche between the in-sample and out-of-sample datasets in order that we are able to concentrate on understanding the core idea of this text.

You should utilize any yfinance ticker to obtain knowledge for an asset of your liking. You too can alter the dates to fit your wants.

Retrospective Simulation utilizing Brownian Bridge

The following half is the principle crux of this weblog. That is the place I simulate the attainable paths the asset may have taken from January 2000 to November 2020. I’ve simulated 1000 paths. You possibly can modify it to make it 100 or 10000, as you want. The upper the worth, the better our confidence within the outcomes, however there’s a tradeoff in computational time. I’ve simulated solely the closing costs. I saved the first-day and last-day costs the identical because the realised ones, and simulated the in-between costs.

Holding the worth mounted on the primary day is smart. However the final day? If the costs are to observe a random stroll (learn extra), the closing worth ranges of most, if not all, paths needs to be totally different, isn’t it? However I made an assumption right here. Given the environment friendly market speculation, the index would have a good worth by the tip of November 2020, and after transferring on its capricious course, it will converge again to this honest worth.

Why solely November 2020?

Was the extent of the index at its fairest worth at the moment? No means of realizing. Nevertheless, one date is nearly as good as every other, and we have to work with a selected date, so I selected this one.

One other consideration right here is on what foundation we permit the simulated paths to meander. Ought to or not it’s parametric, the place we assume the time collection to observe a selected distribution, or non-parametric, the place we don’t make any such assumption? I selected the latter. The monetary literature discusses costs (and their returns) as belonging roughly to sure underlying distributions. Nevertheless, in relation to outlier occasions, akin to extremely risky worth jumps, these assumptions start to interrupt down, and it’s these occasions {that a} quant (dealer, portfolio supervisor, investor, analyst, or researcher) needs to be ready for.

For the non-parametric method, I’ve modified the Brownian bridge method. In a pure Brownian bridge method, the returns are assumed to observe a Gaussian distribution, which once more turns into considerably parametric (learn extra). Nevertheless, in our method, we calculate the realized returns from the in-sample closing costs and use these returns as a pattern for the simulation generator to select from. We’re utilizing bootstrapping with substitute (learn extra), which implies that the realized returns aren’t simply being shuffled; some values could also be repeated, whereas some will not be used in any respect. If the values are merely shuffled, all simulated paths would land on the final closing worth of the in-sample knowledge. How can we be certain that the simulated costs converge to the ultimate shut worth of the in-sample knowledge?  We’ll use geometric smoothing for that.

One other consideration: since we use the realized returns, we’re priming the simulated paths to resemble the realized path, appropriate? Kind of, but when we have been to generate pseudo-random numbers for these returns, we must make some assumption about their distribution, making the simulation a parametric course of.

Right here’s the code for the simulations:

Be aware that I didn’t use a random seed when producing the simulated paths. I’ll point out the explanation at a later stage.

Let’s plot the simulated paths:

The above graph reveals that the beginning and ending costs are the identical for all 1,000 simulated paths. We should always observe one factor right here. Since we’re working with knowledge from a broad market index, whose ranges rely on many interlinked macroeconomic variables and components, it is extremely unlikely that the index would have traversed a lot of the paths simulated above, given the identical macroeconomic occasions that occurred throughout the simulation interval. We’re making an implicit assumption right here that the desired macroeconomic variables and components differ in every of the simulated paths, and the interactions between these variables and components outcome within the simulated ranges that we generate. This holds for every other asset class or asset you determine to interchange the SENSEX index with, for retrospective simulation functions.

Exponential Transferring Common Crossover Technique Improvement and Backtesting on In-Pattern Information, and Parameter Optimisation

Subsequent, we develop a easy buying and selling technique and conduct a backtest utilizing the in-sample knowledge. The technique is a straightforward exponential transferring common crossover technique, the place we go lengthy when the short-period exponential transferring common (SEMA) of the shut worth goes above the long-period exponential transferring common (LEMA), and we go quick when the SEMA crosses the LEMA from above (learn extra).

By optimisation, we’ll try to seek out one of the best SEMA and LEMA mixture that yields the utmost returns. For the SEMA, I exploit lookback durations of 5, 10, 15, 20, … as much as 100, and for the LEMA, 20, 30, 40, 50, … as much as 300.

The situation is that for any given SEMA and LEMA mixture, the LEMA lookback interval needs to be better than the corresponding SEMA lookback interval. We might carry out backtests on all totally different combos of those SEMA and LEMA values and select the one which yields one of the best efficiency.

We’ll plot:

the fairness curve of the technique with the best-performing SEMA and LEMA lookback values, plotted in opposition to the buy-and-hold fairness,the purchase and promote indicators plotted together with the shut costs of the in-sample knowledge and the SEMA and LEMA traces,the underwater plot of the technique, and,a heatmap of the returns for various LEMA and SEMA calculations.

We’ll calculate:

the SEMA and LEMA lookback values for the best-performing mixture,the entire returns of the technique,the utmost drawdown of the technique, and,the Sharpe ratio of the technique.

We can even overview the highest 10 SEMA and LEMA combos and their respective performances.

Right here’s the code for all the above:

And listed below are the outputs of the above code:

Greatest SEMA: 5, Greatest LEMA: 40

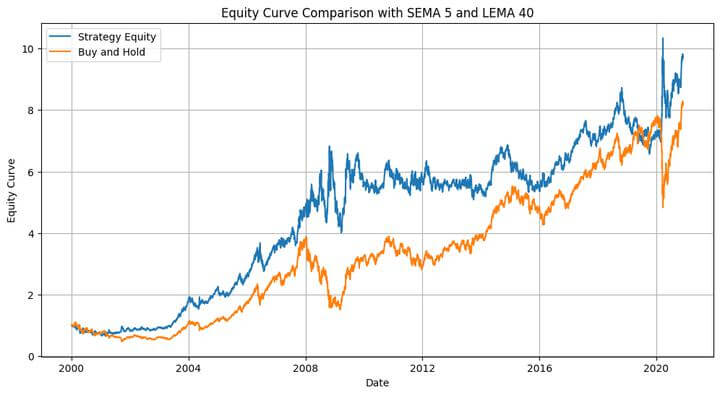
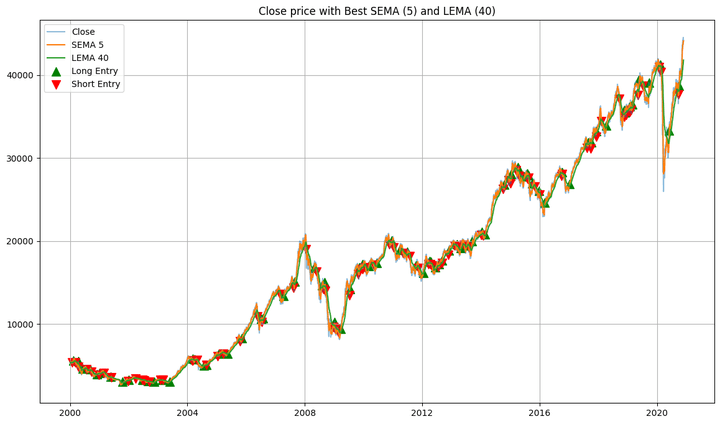
Whole Return: 873.43%
Most Drawdown: -41.28 %
Sharpe Ratio: 0.59

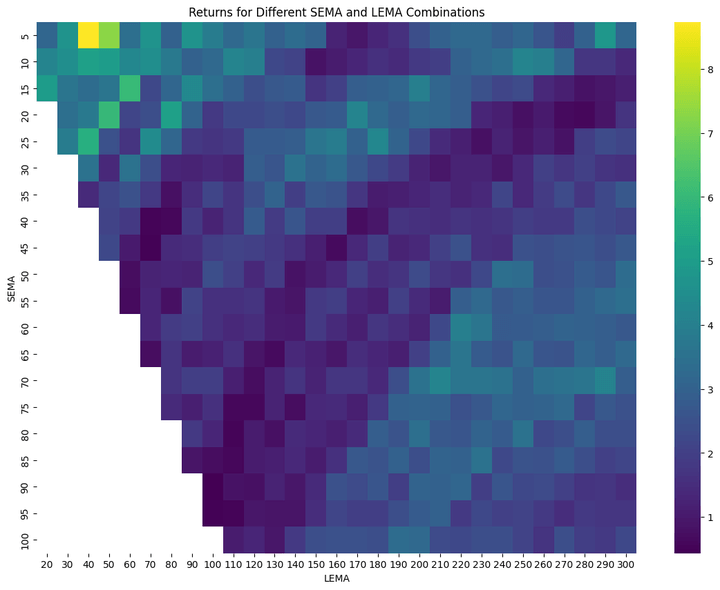
High 10 Parameter Combos:

SEMA LEMA Return
2 5 40 8.734340
3 5 50 7.301270
62 15 60 6.021219
89 20 50 5.998316
116 25 40 5.665505
31 10 40 5.183363
92 20 80 5.071913
32 10 50 5.022373
58 15 20 4.959147
27 5 290 4.794400

The heatmap reveals a gradual change in shade from one adjoining cell to the following. This implies that slight modifications to the EMA values don’t result in drastic modifications within the technique’s efficiency.  In fact, it will be extra gradual if we have been to scale back the spacing between the SEMA values from 5 to, say, 2, and between the LEMA values from 10 to, say, 3.

The technique outperforms the buy-and-hold technique, as proven within the fairness plot. Excellent news, proper? Be aware right here that this was in-sample backtesting. We ran the optimisation on a given dataset, took some data from it, and utilized it to the identical dataset. It’s like utilizing the costs for the following 12 months (that are unknown to us now, besides if you happen to’re time-travelling!) to foretell the costs over the following 12 months. Nevertheless, we are able to utilise the data gathered from this dataset to use it to a different dataset. That’s the place we use the out-of-sample knowledge.

Backtesting on Out-of-Pattern Information

Let’s run the backtest on the out-of-sample dataset:

Earlier than we see the outputs of the above codes, let’s listing what we’re doing right here.

We’re plotting:

The fairness curve of the technique plotted alongside that of the buy-and-hold, and,The underwater plot of the technique.

We’re calculating:

Technique returns,Purchase-and-hold returns,Technique most drawdown,Technique Sharpe ratio,Purchase-and-hold Sharpe ratio, and,Technique hit ratio.

For the Sharpe ratio calculations, we assume a risk-free price of return of 0. Listed here are the outputs:

Out-of-Pattern Technique Whole Return: 15.46%
Out-of-Pattern Purchase-and-Maintain Whole Return: 79.41%
Out-of-Pattern Technique Most Drawdown: -15.77 %
Out-of-Pattern Technique Sharpe Ratio: 0.30
Out-of-Pattern Purchase-and-Maintain Sharpe Ratio: 0.56
Out-of-Pattern Hit Ratio: 53.70%

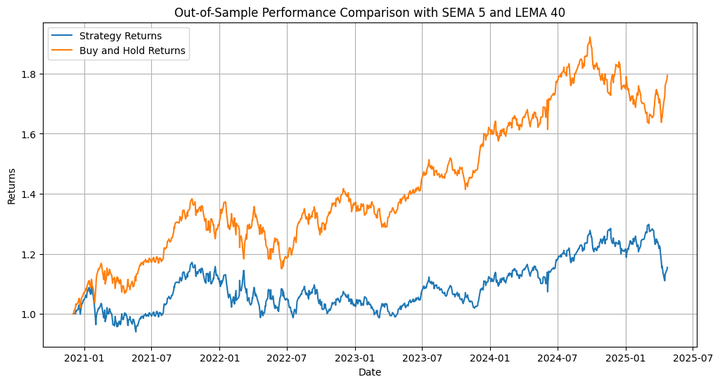
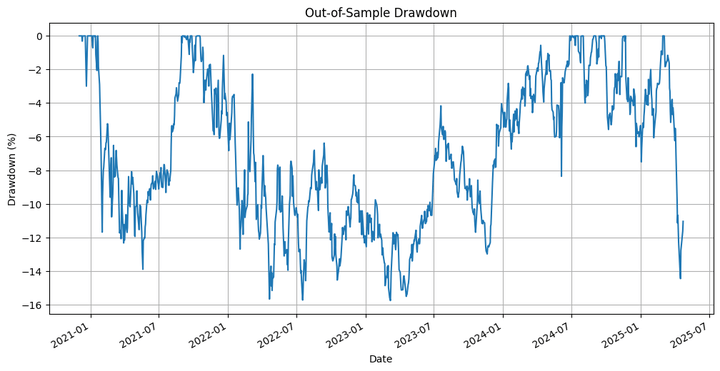
The technique underperforms the underlying by a major margin. However that’s not what we’re primarily interested by, so far as this weblog is worried. We have to take into account that we ran an optimisation on solely one of many many paths that the costs may have taken throughout the in-sample interval, after which extrapolated that to the out-of-sample backtest. That is the place we use the simulation we carried out firstly. Let’s run the backtest on the totally different simulated paths and test the outcomes.

Backtesting on Simulated Paths and Optimising to Extract the Greatest Parameters

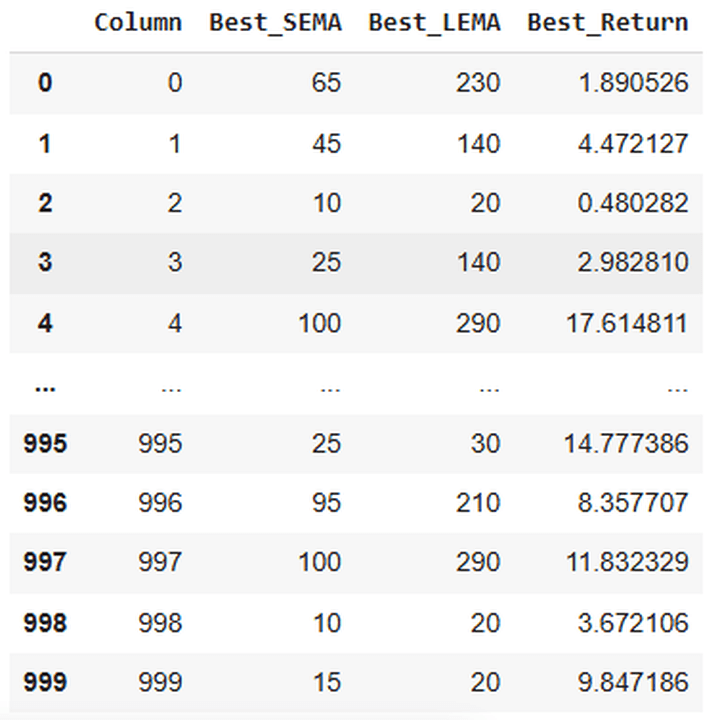
This might maintain printing the corresponding SEMA and LEMA values for one of the best technique efficiency, and the efficiency itself for the simulated paths:

Accomplished optimization for column 0: SEMA=65, LEMA=230, Return=1.8905
Accomplished optimization for column 1: SEMA=45, LEMA=140, Return=4.4721
……………………………………………………………
Accomplished optimization for column 998: SEMA=10, LEMA=20, Return=3.6721
Accomplished optimization for column 999: SEMA=15, LEMA=20, Return=9.8472

Right here’s a snap of the output of this code:

Now, we’ll kind the above desk in order that the SEMA and LEMA mixture with one of the best returns for probably the most paths is on the high, adopted by the second-best mixture, and so forth.

Let’s test how the desk would look:

Right here’s a snapshot of the output:

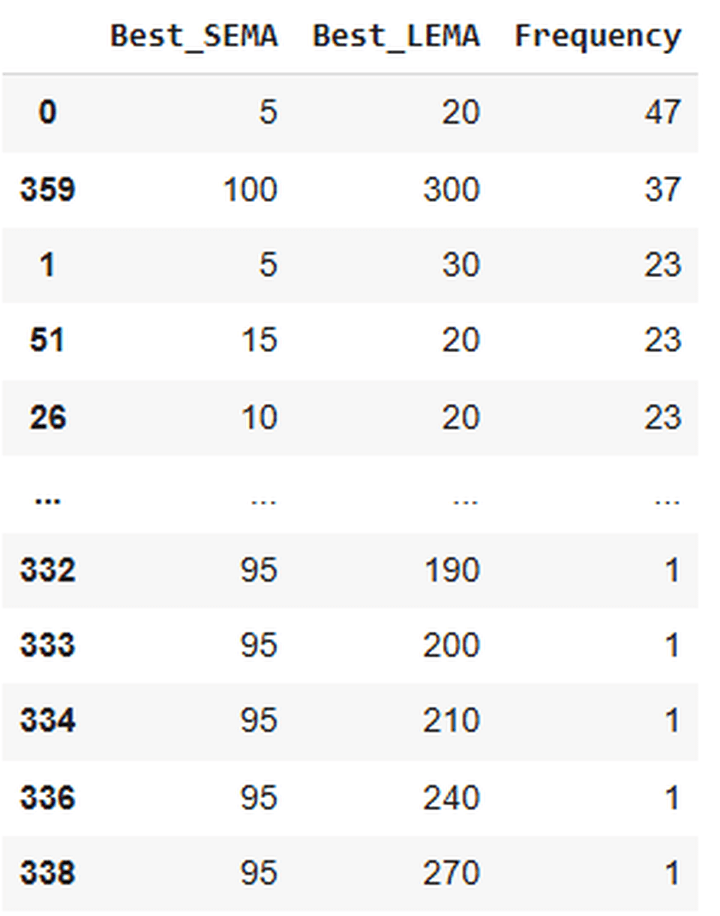
Of the 1000 paths, 47 confirmed one of the best returns with a mix of SEMA 5 and LEMA 20. Since I didn’t use a random seed whereas producing the simulated paths, you’ll be able to run the code a number of occasions and acquire totally different outputs or outcomes. You’ll see that one of the best SEMA and LEMA mixture within the above desk would almost definitely be 5 and 20. The frequencies can change, although.

How do I do know?

As a result of I’ve finished so, and have gotten the mix of 5 and 20 within the first place each time (adopted by 100 and 300 within the second place). In fact, it’s not that there’s a zero likelihood of getting another mixture within the high row.

Out-of-Pattern Backtesting utilizing Optimised Parameters primarily based on Simulated Information Backtesting

We’ll extract the SEMA and LEMA look-back mixture from the earlier step that yields one of the best returns for a lot of the simulated paths. We’ll use a dynamic method to automate this choice. Thus, if as a substitute of 5 and 20, we have been to acquire, say, 90 and 250 because the optimum mixture, the identical could be chosen, and the backtest could be carried out utilizing that.

Let’s use this mix to run an out-of-sample backtest:

Listed here are the outputs:

Out-of-Pattern Technique Whole Return: -7.73%
Out-of-Pattern Purchase-and-Maintain Whole Return: 79.41%
Out-of-Pattern Technique Most Drawdown: -23.70 %
Out-of-Pattern Technique Sharpe Ratio: -0.05
Out-of-Pattern Purchase-and-Maintain Sharpe Ratio: 0.56
Out-of-Pattern Hit Ratio: 52.50%

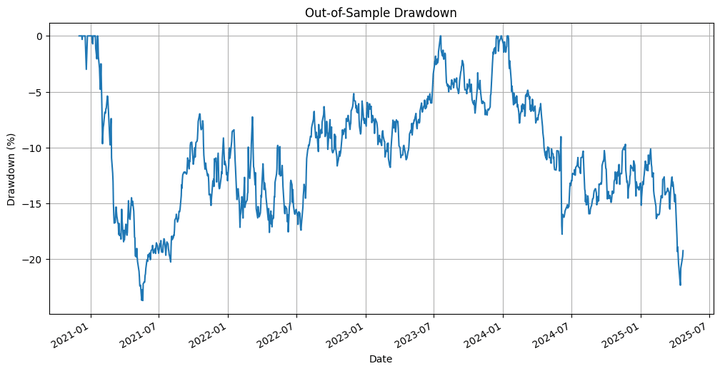
Dialogue on the Outcomes and the Strategy

Right here, the technique not solely underperforms the underlying but in addition generates damaging returns. So what’s the purpose of all this effort that we put in? Let’s observe that I employed the transferring common crossover technique to illustrate the applying of retrospective simulation utilizing a modified Brownian bridge. This method is extra appropriate for testing complicated methods with a number of situations, and machine studying (ML)-based and deep studying (DL)-based methods.

We’ve got approaches akin to walk-forward optimisation and cross-validation to beat the issue of optimising or fine-tuning a technique or mannequin on solely one of many many attainable traversable paths.

Nevertheless, this method of retrospective simulation ensures that you simply don’t need to depend on just one path however can make use of a number of retrospective paths. Nevertheless, since operating an ML-based technique on these simulated paths could be too computationally intensive for many of our readers who don’t have entry to GPUs or TPUs, I selected to work with a easy technique.

Moreover, if you happen to want to modify the method, I’ve included some options on the finish.

Analysis of VaR and C-VaR

Let’s transfer on to the following half. We’ll utilise the retrospective simulation to calculate the worth in danger and the conditional worth in danger (learn extra: 1, 2, 3).

Output:

Worth at Danger – 90%: -0.014976172535594811
Worth at Danger – 95%: -0.022113806787530325
Worth at Danger – 99% -0.04247765359038646
Anticipated Shortfall – 90%: -0.026779592114352924
Anticipated Shortfall – 95%: -0.035320511964199504
Anticipated Shortfall – 99% -0.058565593363193474

Let’s decipher the above output. We first calculated the day by day p.c returns of all 1000 simulated paths. Each path has 5,155 days of knowledge, which yielded 5,154 returns per path. When multiplied by 1,000 paths, this resulted in 5,154,000 values of day by day returns. We used all these values and located the bottom ninetieth, ninety fifth, and 99th percentile values, respectively.

From the above output, for instance, we are able to say with 95% certainty that if the longer term costs observe paths just like these simulated paths, the utmost drawdown that we are able to face on any given day could be 2.21%. The anticipated drawdown could be 3.53% if that stage will get breached.

Let’s discuss concerning the extremes now. Let’s examine the utmost and minimal day by day returns of the simulated paths and the realised in-sample path.

Realized Lowest Day by day Return: -0.1315258002691394
Realized Highest Day by day Return: 0.17339334818061447

The utmost values from each approaches are shut, at round 17.4%. Similar for the minimal values, at round -13.2%. This makes a case for utilizing this method in monetary modelling.

Distribution of Simulated Information

Let’s see how the simulated returns are distributed and examine them visually to a standard distribution. We’ll additionally calculate the skewness and the kurtosis.

Skewness: -0.11595652411010503
Kurtosis: 9.597364213156881

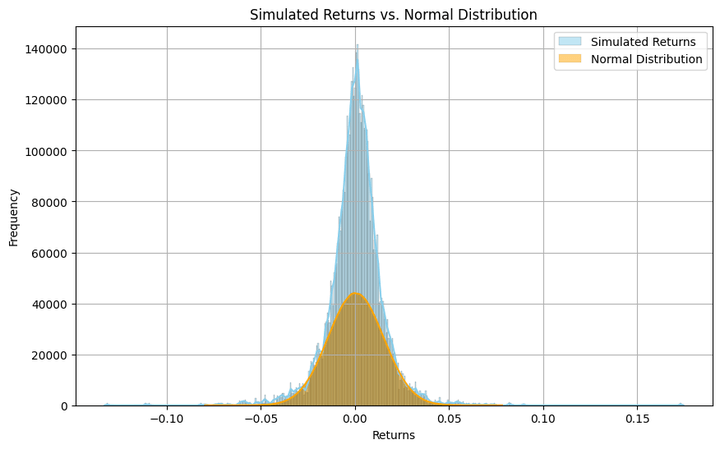
The argument ‘kde’, when set to ‘True’, smooths the histogram curve, as proven within the above plot. Additionally, in order for you a extra granular (coarse) visible of the distribution, you’ll be able to improve (scale back) the worth within the ‘bins’ argument.

Although the histogram resembles a bell curve, it’s removed from a standard distribution. It reveals heavy kurtosis, that means there are vital possibilities of discovering returns which are many commonplace deviations away from the imply. And this isn’t any shock, since that’s how fairness and equity-index returns are inherently.

The place This Strategy Can Be Most Helpful

Whereas the technique I used right here is straightforward and illustrative, this retrospective simulation framework comes into its personal when utilized to extra complicated or nuanced methods. It’s helpful in instances the place:

You are testing multi-condition or ML-based fashions which may overfit on a single realized path.You need to stress take a look at a technique throughout alternate historic realities—ones that didn’t occur, however very nicely may have.Conventional walk-forward or cross-validation strategies don’t appear to be sufficient, and also you need an added lens to guage generalisability.You are exploring how a technique may behave (or may need behaved had the worth taken on any alternate worth path) beneath excessive market strikes that aren’t current within the precise historic path.

In essence, this technique lets you transition from “what occurred” to “what may have occurred,” a refined but highly effective shift in perspective.

Recommended Subsequent Steps

If you happen to discovered this method attention-grabbing, listed below are a number of methods you’ll be able to lengthen it:

Attempt extra refined methods: Apply this retrospective simulation to mean-reversion, volatility breakout, or reinforcement learning-based methods.Introduce macro constraints: Anchor the simulations round recognized macroeconomic markers or regime modifications to check how methods behave in such environments.Use intermediate anchor factors: As an alternative of simply fixing the beginning and finish costs, strive anchoring the simulation at quarterly or annual ranges to higher management drift and convergence.Practice ML fashions on simulated paths: If you happen to’re working with supervised studying or deep studying fashions, prepare them on a number of simulated realities as a substitute of 1.Portfolio-level testing: Use this framework to guage VaR, CVaR, or stress-test a whole portfolio, not only a single technique.

That is only the start—the way you construct on it will depend on your curiosity, computing sources, and the questions you are making an attempt to reply.

In Abstract

The weblog launched a retrospective simulation framework utilizing a non-parametric Brownian bridge method to simulate alternate historic worth paths.We employed a easy EMA crossover technique to illustrate how this simulation could be built-in into a conventional backtesting loop.We extracted one of the best SEMA and LEMA combos after operating backtests on the simulated in-sample paths, after which used these for backtesting on the out-of-sample knowledge.This simulation technique allows us to check how methods would behave not solely in response to what occurred, but in addition in response to what may have occurred, serving to us keep away from overfitting and uncover strong indicators.The identical simulated paths can be utilized to derive distributional insights, akin to tail danger (VaR, CVaR) or return extremes, providing a deeper understanding of the technique’s danger profile.

Continuously Requested Questions

1. Curious why we simulate worth paths in any respect?Actual market knowledge reveals just one path the market took, amongst many attainable paths. However what if we need to perceive how our technique would behave throughout many believable realities sooner or later, or would have behaved throughout such realities prior to now? That’s why we use simulations.

2. What precisely is a Brownian bridge, and why was it used?A Brownian bridge simulates worth actions that begin and finish at particular values, like actual historic costs. This helps guarantee simulated paths are anchored in actuality whereas nonetheless permitting randomness in between. The principle query we ask right here is “What else may have occurred prior to now?”.

3. What number of simulated paths ought to I generate to make this evaluation significant?We used 1000 paths. As talked about within the weblog, when the variety of simulated paths will increase, computation time will increase, however our confidence within the outcomes grows too.

4. Is that this solely for easy methods like transferring averages?By no means. We used the transferring common crossover simply for instance. This framework could be (and needs to be) used if you’re testing complicated, ML-based, or multi-condition methods which will overfit to historic knowledge.

5. How do I discover one of the best parameter settings (like SEMA/LEMA)?For every simulated path, we backtested totally different parameter combos and recorded the one which gave the very best return. By counting which combos carried out finest throughout most simulations, we recognized the mix that’s almost definitely to carry out nicely. The thought is to not depend on the mix that works on only one path.

6. How do I do know which parameter combo to make use of within the markets?The thought is to select the combo that the majority ceaselessly yielded one of the best outcomes throughout many simulated realities. This helps keep away from overfitting to the only historic path and as a substitute focuses on broader adaptability. The precept right here is to not let our evaluation and backtesting be topic to likelihood or randomness, however slightly to have some statistical significance.

7. What occurs after I discover that “finest” parameter mixture?We run an out-of-sample backtest utilizing that mixture on knowledge the mannequin hasn’t seen. This checks whether or not the technique works outdoors of the information on which the mannequin is skilled.

8. What if the technique fails within the out-of-sample take a look at?That’s okay, and on this instance, it did! The purpose is to not “win” with a fundamental technique, however to indicate how simulation and strong testing reveal weaknesses earlier than actual cash is concerned. In fact, if you backtest an precise alpha-generating technique utilizing this method and nonetheless get underperformance within the out-of-sample, it seemingly implies that the technique isn’t strong, and also you’ll have to make modifications to the technique.

9. How can I exploit these simulations to know potential losses?We adopted the method of flattening the returns from all simulated paths into one massive distribution and calculating danger metrics like Worth at Danger (VaR) and Conditional VaR (CVaR). These present how unhealthy issues can get, and the way usually.

10. What’s the distinction between VaR and CVaR?

VaR tells us the worst anticipated loss at a given confidence stage (e.g., “you’ll lose not more than 2.2% on 95% of days”).CVaR goes a step additional and says, “If you happen to lose greater than that, right here’s the common of these worst days.”.

11. What did we study from the VaR/CVaR outcomes on this instance?We noticed that 99% of days resulted in losses no worse than ~4.25%. However when losses exceeded that threshold, they averaged ~5.86%. That’s a helpful perception into tail danger. These are the uncommon however extreme occasions that may extremely have an effect on our buying and selling accounts if not accounted for.

12. Are the simulated return extremes practical in comparison with actual markets?Sure, they matched very carefully with the utmost and minimal day by day returns from the true in-sample knowledge. This validates that our simulation isn’t simply random however is grounded in actuality.

13. Do the simulated returns observe a standard distribution?Not fairly. The returns confirmed excessive kurtosis (fats tails) and slight damaging skewness, that means excessive strikes (each up and down) are extra widespread than a standard distribution would have. This mirrors actual market behaviour.

14. Why does this matter for danger administration?If our technique assumes regular returns, we’re closely underestimating the likelihood of serious losses. Simulated returns reveal the true nature of market danger, serving to us put together for the sudden.

15. Is that this simply an educational train, or can I apply this virtually? This method is extremely helpful in apply, particularly if you’re working with:

Machine studying fashions which are  vulnerable to overfittingStrategies designed for high-risk environmentsPortfolios the place stress testing and tail danger are crucialRegime-switching or macro-anchored fashions

It helps shift our mindset from “What labored earlier than?” to “What would have labored throughout many alternate market situations?”, and that may be one latent supply of alpha.

Conclusion

Hope you discovered at the very least one new factor from this weblog. If that’s the case, do share what it’s within the feedback part under and tell us if you happen to’d prefer to learn or study extra about it. The important thing takeaway from the above dialogue is the significance of performing simulations retrospectively and making use of them to monetary modelling. Apply this method to extra complicated methods and share your experiences and findings within the feedback part. Blissful studying, completely satisfied buying and selling 🙂

Credit

José Carlos Gonzáles Tanaka and Vivek Krishnamoorthy, thanks to your meticulous suggestions; it helped form this text!

Chainika Thakar, thanks for rendering and publishing this, and making it obtainable to the world, that too in your birthday!

Disclaimer: All investments and buying and selling within the inventory market contain danger. Any resolution to position trades within the monetary markets, together with buying and selling in inventory or choices or different monetary devices is a private resolution that ought to solely be made after thorough analysis, together with a private danger and monetary evaluation and the engagement {of professional} help to the extent you consider essential. The buying and selling methods or associated data talked about on this article is for informational functions solely.